Растворы неэлектролитов

РАСТВОРЫ НЕЭЛЕКТРОЛИТОВ, бинарные или многокомпонентные мол. системы, состав к-рых может изменяться непрерывным образом (по крайней мере, в нек-рых пределах). В отличие от растворов электролитов, в Р. н. (мол. р-рах) заряженные частицы в сколько-нибудь заметных концентрациях отсутствуют. Р. н. могут быть твердыми, жидкими и газообразными. В данной статье рассматриваются жидкие р-ры; см. также Твердые растворы.

Взаимная р-римость двух жидкостей при заданных т-ре Т и давлении р м. б. полной (неограниченной) или ограниченной. В последнем случае р-ры в нек-рой области составов расслаиваются, т. е. разделяются на две жидкие фазы, отличающиеся по концентрации. В многокомпонентных расслаивающихся р-рах число сосуществующих жидких фаз м. б. более двух. Если один (или более) из компонентов Р.н. в чистом состоянии при заданных Т и р является газом или твердым телом, область существования Р.н. простирается от чистой жидкости (смеси жидкостей), выступающей в роли р-рителя, до состава, отвечающего насыщ. р-ру.

Р.н. служат средой, в к-рой протекают многие прир. и пром. процессы. Изучение и прогнозирование св-в этих систем тесно связаны с такими практич. проблемами, как подбор р-рителей для реализации технол. процессов, получение систем с заданными св-вами, разделение прир. и пром. смесей (включая газы и нефти), глубокая очистка в-в.

Физ. химия изучает широкий диапазон св-в р-ров. Наиб. разработана и имеет практически важные применения равновесная термодинамика р-ров; дальнейший материал посвящен в осн. этому разделу физ. химии р-ров. Кроме того, изучаются транспортные св-ва р-ров-диффузия, теплопроводность, вязкость (см. Физико-химическая гидродинамика), а также спектроскопич., электрич., акустич. и др. физ. св-ва. Методы исследования макроскопич. св-в Р. н. и их структурных характеристик во многом аналогичны методам исследования индивидуальных жидкостей, но осн. внимание уделяется рассмотрению концентрац. зависимостей св-в. Важнейшая задача физ.-хим. исследований - установление связи между наблюдаемыми на опыте св-вами, структурой р-ров и характеристиками межмолекулярных взаимодействий. Эксперим. информацию о структуре р-ров и межмолекулярных взаимод. в них дают методы оптической и радиоспектроскопии, дифракционные, электрич. и др. Важную роль в изучении Р.н. играет физико-химический анализ, основанный на построении и исследовании фазовых диаграмм, концентрац. зависимостей термодинамич. и др. физ. св-в (показателя преломления, вязкости, теплопроводности, акустич. характеристик и др.). При этом одна из главных задач состоит в том, чтобы на основании анализа диаграмм состав - свойство устанавливать факт образования хим. соединений между компонентами Р.н. и находить их характеристики.

Значит. влияние на физ. св-ва р-ров (в частности, на рассеяние света) оказывают флуктуации плотности, концентрации, ориентации молекул. Роль флуктуации концентрации особенно велика вблизи критич. точки р-римости (см. Критические явления).

Концентрационные зависимости термодинамических функций. Особенностью термодинамич. описания Р. н. по сравнению с чистыми компонентами является наличие дополнит. термодинамич. степеней свободы системы, связанных с возможностью изменения состава системы (см. Фаз правило). Число степеней свободы гомогенного n-компонентного р-ра равно n+1. В качестве переменных, определяющих его состояние, наиб. удобно выбрать давление р, т-ру Т и концентрации п — 1 компонентов. Состав Р. н. чаще всего выражают через молярные доли компонентов x_i, считая независимыми переменными молярные доли всех компонентов, кроме n-го x₁,..., x_n-1. Для задания концентрации используют и др. шкалы (молярности с, моляльности т).

При описании концентрац. зависимостей термодинамич. ф-ций важную роль играют парциальные молярные величины M_i для i-го компонента, определяемые соотношением:

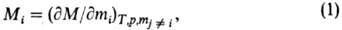
где М-любая экстенсивная термодинамич. ф-ция (объем V, внутр. энергия U, энтальпия H, энтропия S, энергии Гельм-гольца и Гиббса F и G, теплоемкость С_р и т.д.), m_i-число молей. Важнейшая парциальная молярная величина -химический потенциал m_i (парциальная молярная энергия Гиббса); именно через хим. потенциалы формулируются условия хим. и фазового равновесий в системе.

Концентрац. зависимость термодинамич. св-в Р. н. нередко характеризуют функциями смешения М^т - изменением термодинамич. ф-ции М при образовании р-ра из чистых жидкостей. Рассматривают смешение при изотермо-изобар-ных (Т, р = const) или изотермо-изохорных (Т, V = const) условиях, причем наиб. практич. интерес представляет случай Т, р — const. Молярная ф-ция смешения при этих условиях (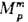) определена соотношением:

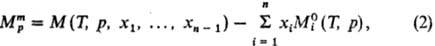
где 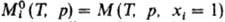-молярное значение ф-ции M для чистой жидкости i при заданных Т и р. В частности, молярная энергия Гиббса смешения

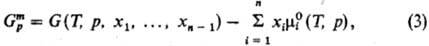
где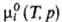-хим. потенциал чистой жидкости i при заданных Т и р. Для чистых жидкостей 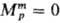(рис., а). Поскольку образование р-ра при смешении жидкостей - самопроизвольный процесс, то G^m < 0.

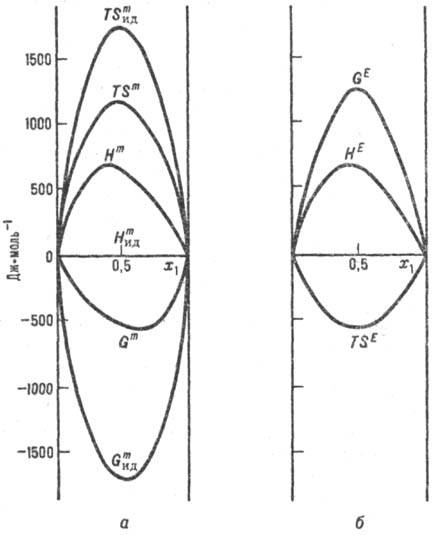
Функции смешения для реального и идеального р-ров (а) и избыточные термо-динамич. функции (б). Система пропанол - циклогексан, 298,5 К; x₁-молярная доля пропанола.

Парциальная молярная ф-ция смешения имеет вид:

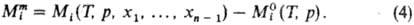
Термодинамич. соотношения, связывающие величины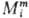и М^m между собой и с др. термодинамич. параметрами, аналогичны соотношениям, связывающим M_i и М. Так,

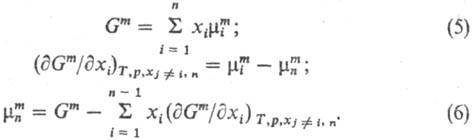
Зависимости энергии смешения Гиббса и хим. потенциалов смешения от т-ры и давления выражаются соотношениями:

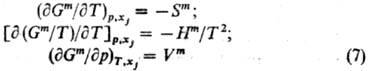
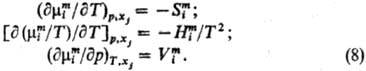
Вдали от критич.точки равновесия жидкость-пар влияние давления на ф-ции смешения жидкого р-ра, как правило, незначительно и им нередко пренебрегают.

Идеальные растворы. Имеется неск. по существу идентичных определений идеального р-ра. Согласно одному из наиб. удобных, это р-р, хим. потенциалы компонентов к-рого во всей областиконцентраций отвечают ур-нию:

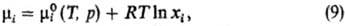
где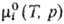-хим. потенциал чистой жидкости i при тех же давлении и т-ре, что и рассматриваемый р-р, R-газовая постоянная. Ф-ции смешения идеального р-ра:

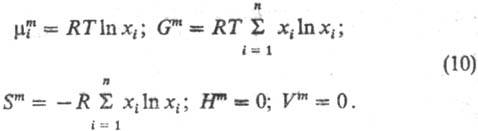
При образовании идеального р-ра энергетич. изменений не происходит, изменяются только энтропия системы и энтропийные составляющие термодинамич. ф-ций.

Если р-р идеальный, а равновесный с ним пар ведет себя как идеальный газ, выполняется Рауля закон:

где p_i-парциальное давление i-го компонента над р-ром, 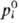-давление насыщ. пара чистой жидкости при рассматриваемой т-ре.

Идеальный р-р-гипотетич. система, компоненты к-рой одинаковы по характеристикам межмол. взаимодействий. Так, для бинарного р-ра одинаковыми должны быть потенциалы парного взаимод. компонентов 1 и 2 u₁₁, и₂₂ и u₁₂ (форма потенциалов м. б. любой; в частности, не исключается возможность специфич. взаимод. компонентов 1-1, 2-2 и 1-2 одинаковой интенсивности). При выполнении указанного требования смешение жидкостей не сопровождается энергетич. изменениями. Т.к. число разл. конфигураций в результате смешения увеличивается в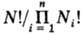раз (N_i- число частиц i-го сорта, N = SN_i), то энтропия смешения 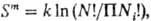где k-постоянная Больцмана; получаем ф-лы (10).

Поведение, близкое к идеальному, обнаруживают р-ры, образованные молекулами разл. изотопного состава (напр., С₆Н₁₂ и C₆D₁₂), оптич. изомерами, соседними гомологами с большой длиной цепи (напр., алканами С₂₅ и С₂₆) и т.д.

Бесконечно разбавленные Р. н. Р-р наз. бесконечно разбавленным по компоненту i, если x_i:0. Для определенности будем говорить о бинарном р-ре 1-2 при х₂:0 (1-р-ри-тель, 2-растворенное в-во). Особенность такого р-ра состоит в том, что молекулы растворенного в-ва окружены лишь молекулами р-рителя; взаимод. между молекулами растворенного в-ва (типа 2-2)отсутствуют, существенны лишь взаимод. типа 1-1 и 1-2. Пока р-р остается бесконечно разбавленным и взаимод. 2-2 не проявляются, добавляемые молекулы 2 попадают в среднем в одинаковые условия взаимод. с окружением и каждая дополнительно вносимая молекула дает такой же вклад в среднюю энергию системы, объем и др. св-ва, как и предыдущие. Парциальные молярные энергетич. характеристики р-ра остаются неизменными, и концентрац. зависимость хим. потенциалов компонентов определяется чисто энтропийным вкладом RTlnx_i, как и в случае идеального р-ра. Т. обр., при x₂:0

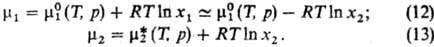
Здесь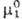-хим. потенциал чистого р-рителя. Стандартный хим. потенциал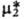относится к гицотетич. чистой жидкости 2, в к-рой компонент 2 обладает теми же парциальными молярными энергетич. св-вами, что и в бесконечно разб. р-ре.

При х₂ : 0 m₂ : — ,; S₂ : ,; предельные значения парциальных внутр. энергии, энтальпии, объема растворенного в-ва конечны.

Для бесконечно разб. р-ров выполняется ряд простых количеств. закономерностей, к-рые получили назв. законов разб. р-ров. Это закон Рауля (11) для р-рителя и Генри закон для растворенного в-ва р₂ = К_гх₂, где р₂ - парциальное давление пара растворенного в-ва, x₂-его молярная доля в р-ре, К_г - постоянная Генри; закон Вант-Гоффа для осмо-тич. давления p = RTc, где p-осмотич. давление, с-молярная концентрация растворенного в-ва (см. Осмос); закономерности понижения т-ры замерзания р-ров и повышения т-ры их кипения, если растворенное в-во нелетуче. Для данного р-рителя при фиксированных Т и р давление пара, осмотич. давление, т-ры кипения и замерзания р-ра оказываются зависящими только от концентрации растворенного в-ва, но не от его природы, что объединяет названные св-ва в общее понятие коллигативных.

Важной характеристикой бесконечно разб. р-ров являются функции сольватации-изменения термодинамич. ф-ций (энергии, энтальпии, стандартной парциальной энтропии, стандартного хим. потенциала и др.) при переносе растворенного в-ва из идеальной газовой фазы в бесконечно разб. р-р. Ф-ции сольватации несут количеств. информацию об интенсивности взаимод. молекул растворенного в-ва с р-ри-телем.

Термодинамические характеристики неидеальных Р.н.

Неидеальные Р.н. часто характеризуют т. наз. избыточными термодинамическими функциями М^E, к-рые представляют собой разность между ф-циями смешения реального и идеального р-ров одинаковой концентрации (рис., б). Обычно эти ф-ции относят к процессу смешения при р,Т= const, реже-при V, Т= const. С учетом выражений (10) получаем:

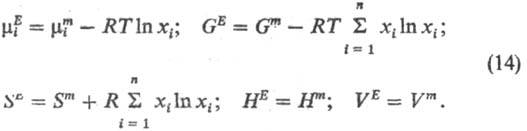
Для представления концентрац. зависимости хим. потенциала i-го компонента реального р-ра вводят величину a_i, наз. термодинамич. активностью:

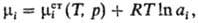
где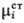-стандартный хим. потенциал. В стандартном состоянии a_i= 1. Если в качестве стандартного состояния для всех компонентов принимают соответствующие чистые жидкости (симметричный способ нормировки), то 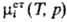= =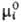(Т,р). При нормировке, наз. несимметричной, стандартное состояние для р-рителя, как и в предыдущем случае,-чистая жидкость, но для растворенного в-ва (компонент 2)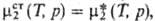причем в шкале молярных долей величина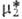определена так же, как в ф-ле (13). Стандартное состояние в шкалах молярности и моляльности отвечает соответствующим единичным концентрациям.

Коэффициенты активности g_i = a_i/x_i = 1 при симметричном способе нормировки для чистых жидкостей (x_i = 1). При несимметричном способе нормировки коэффициенты активности и р-рителя и растворенного в-ва равны единице в бесконечно разб. р-ре: g₁ (х₂= 0) = g₂(x₂ = 0) = 1. В случае симметричной нормировки

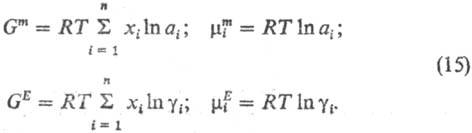
В зависимости от знака избыточной энергии Гиббса G^E говорят о положит. или отрицат. отклонениях от идеального поведения.

При анализе концентрац. зависимостей хим. потенциалов (активностей, коэф. активностей) важную роль играет Гиббса -Дюгема уравнение. В соответствии с этим ур-нием при Т, р = const

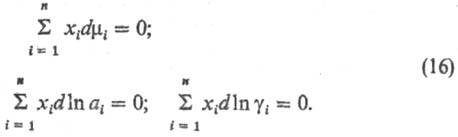
Условия устойчивости р-ра относительно непрерывных изменений параметров состояния требуют, чтобы при заданных Тир кривизна пов-сти G(x₁, ..., х_n-1) была положительной. Для бинарного р-ра это сводится к условию: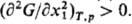Если неравенство выполняется во всей области составов, жидкости обладают полной взаимной р-римостью. Если в к.-л. области составов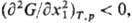 взаимная р-римость ограничена, наблюдается расслаивание р-ра. На границе устойчивости р-ра относительно непрерывных изменений параметра состояния (на спинодали) В критич. точке р-римости бинарной системы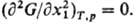выполняется записанное равенство, а также равенство 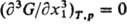(см. Критическое состояние).

Межмолекулярные взаимодействия в растворах. Особенности концентрационных и температурных зависимостей термодинамич. св-в р-ров определяются характером межмолекулярных взаимодействий между одноименными и разноименными частицами: природой и интенсивностью сил притяжения (дисперсионных, индукц., ориентац., донорно-ак-цепторных), размерами и формой молекул, т.е. видом потенциала отталкивания. Учет размеров молекул оказывается чрезвычайно существенным для объяснения св-в растворов полимеров; далее речь пойдет гл. обр. о р-рах низко-мол. в-в.

С учетом характера сил притяжения можно выделить след, типы бинарных р-ров: 1) р-ры, образованные неполярными компонентами (смеси сжиженных благородных газов, мн. двухатомных газов, смеси углеводородов, перфторугле-водородов); 2) р-ры, содержащие полярный и неполярный компоненты; 3) р-ры, образованные двумя полярными компонентами. Кроме того, каждый из этих типов обнаруживает большое разнообразие в мол. св-вах и термодинамич. поведении. К системам второго и третьего типа относят, в частности, ассоциир. р-ры, в к-рых специфич. взаимод. приводят к образованию мол. комплексов из одинаковых молекул (ассоциаты) или разных (сольваты). Наиб. распространенным случаем специфич. взаимод. в Р. н. является водородная связь.

Ассоциаты из одинаковых молекул А_i (i = 2, 3 ...) образуются в том случае, если молекула А содержит и электро-нодонорные (протоноакцепторные) и электроноакцепторные (протонодонорные) группы (спирты, карбоновые к-ты и др.). Если молекулы В содержат такие группы (хотя бы одного типа), молекулы А образуют с ними смешанные ассоциаты, если не содержат, то ассоциаты не образуются. Если молекула А является только донором электронов, а молекула В-только акцептором, в чистых жидкостях ассоциаты отсутствуют, но в р-ре образуются смешанные ассоциаты. Пример такой системы-р-р ацетон-хлороформ. Среди ассоциир. систем особыми св-вами обладают вода и водные р-ры, что в большой степени определяется специфич. структурой воды, наличием пространств. сетки водородных связей, к-рая изменяется под влиянием молекул растворенных в-в.

Для р-ров, образованных двумя неполярными (или двумя полярными) компонентами, могут наблюдаться и положит. и отрицат. отклонения от идеальности, причем положительные встречаются чаще; для нек-рых систем они весьма велики (алкан - перфторалкан, вода-кетон и др.). Для смесей полярного и неполярного компонентов характерны положит. отклонения от идеальности, нередко наблюдается очень малая взаимная р-римость жидкостей (напр., в системах вода-алкан); именно к этому типу относят системы с наиб. отклонениями от идеальности. В ассоциир. р-рах знак и величина избыточных термодинамич. ф-ций определяются в первую очередь изменением числа специфич. связей в р-ре по сравнению с чистыми жидкостями. Определяющая роль хим. взаимод. подчеркивалась Д. И. Менделеевым в его учении о р-рах.

Молекулярная теория растворов. Структура р-ров отличается от структуры чистой жидкости тем, что наряду с локальными неоднородностями плотности и распределения молекул по ориентациям (последнее-в случае нецентральных межмол. сил) в р-рах имеются также концентрац. неоднородности. Локальные корреляции в расположении молекул и их ориентации в р-ре м. б. описаны с помощью мол. ф-ций распределения. В бинарной системе (компоненты 1 и 2) для характеристики распределения частиц в окрестности нек-рой данной частицы на расстоянии r от нее служат радиальные функции распределения g₁₁(r), g₂₂(r), g₁₂(r) = g₂₁(r). Через эти ф-ции можно выразить локальный состав окружения частицы данного сорта. Для систем, между молекулами к-рых действуют нецентральные силы, вводятся корреляционные функции, зависящие от угловых переменных, т.е. от взаимной ориентации молекул.

Статистическая термодинамика дает принципиальную возможность вычислить структурные и термодинамич. св-ва системы исходя из ее мол. характеристик и потенциалов межмол. взаимодействия. Для р-ров, как и для чистых жидкостей, развиваются: 1) аналит. теории, в к-рых связь между корреляц. ф-циями и потенциалом взаимод. получают в виде интегральных ур-ний; 2) методы численного моделирования - Монте-Карло и мол. динамики (см. Молекулярная динамика); 3) возмущений теория; 4) приближенные модельные, в частности решеточные, теории (см. Жидкость).

Теория разб. р-ров Майера-Макмиллана на строгой мол.-статистич. основе рассматривает разложение термодинамич. ф-ций по степеням концентрации или активности растворенного в-ва, дает мол. интерпретацию коэф. разложений, устанавливает аналогию в разложениях для разб. р-ров и для газов (по степеням давления). Помимо подхода, опирающегося на информацию о потенциалах взаимод. и общие идеи мол.-статистич. рассмотрения, для установления связи между термодинамич. и мол. св-вами разб. р-ров развиваются методы, рассматривающие р-ритель как непрерывную среду и применяющие к р-ру представления теории диэлектриков.

Мол.-статистич. теории, ставящие своей задачей вывести структурные и термодинамич. св-ва р-ра из потенциала взаимод. (т. наз. строгие теории), в последние десятилетия достигли больших успехов. Для совр. работ в этой области характерен переход от изучения смесей простых жидкостей (систем с центральными взаимод.) к изучению смесей молекулярных флюидов, т.е. систем, образованных двух-и многоатомными молекулами, где взаимод. обычно носят нецентральный характер из-за асимметрии мол. формы (потенциала отталкивания), наличия электрич. моментов молекул (дипольного, квадрупольного и др.). Большую роль в исследовании мол. флюидов играют теория возмущений и численное моделирование. При этом теория возмущений в большой степени опирается на результаты, полученные для простых систем, в частности для смесей частиц, моделируемых твердыми сферами разного размера, св-ва к-рых хорошо изучены с помощью интегральных ур-ний и численными методами. Развиваются варианты теории возмущений с применением принципа соответств. состояний (теория конформных р-ров).

Исследования, базирующиеся на интегральных ур-ниях, теории возмущений, численном моделировании, относятся в осн. к бинарным р-рам. Для бинарных р-ров с центральными взаимод. при небольших различиях в параметрах потенциалов взаимод. 1-1 и 2-2 теория возмущений дает зависимости избыточных термодинамич. ф-ций от состава, близкие к регулярным, т. е. симметричные по компонентам 1 и 2. В частности,

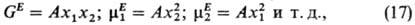
где А -коэф., выражаемый через св-ва стандартной жидкости и параметры потенциалов взаимод. 1-1, 2-2, 1-2.

Приближенные теории р-ров исходят из упрощающих допущений относительно структуры р-ра. Эти теории обычно оперируют параметрами, для определения к-рых требуется эксперим. термодинамич. информация об исследуемой системе. Теория регулярных растворов Скетчарда-Гильдебрандта предложена для р-ров, образованных неполярными жидкостями, молярные объемы к-рых одного порядка (различия не более чем в 2-3 раза). Делается допущение об идеальном значении энтропии смешения при постоянном объеме. Избыточная внутр. энергия определяется выражением:

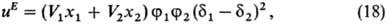
где V_i-молярный объем i-го компонента (i = 1,2), x_i-его молярная доля,-объемная доля, d_i = (E_iисп/V_i)^1/2 параметр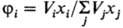растворимости (осн.параметр теории), E_iисп-энергия испарения жидкости.

Решеточные теории основаны на допущении о квази-кристаллич. структуре р-ра, хотя, вообще говоря, при этом преувеличивается аналогия между жидкостью и твердым телом, поскольку жидкости приписывается дальний порядок. Теория строго регулярных р-ров, развитая в работах Э. А. Гуггенгейма и др., относится к системам, образованным частицами примерно одинакового размера, взаимодействующим посредством центр. сил. Осн. параметр тео-рии-энергия взаимообмена

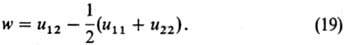
Величина w характеризует различие между энергией взаимод. пары ближайших соседей 1-2 и средним арифметическим энергии однотипных взаимод.:

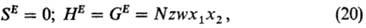
где z-координац. число решетки, N- общее число частиц в системе. Модель находит применение в исследованиях твердых сплавов, расплавов.

Модели атермич. р-ров учитывают влияние размеров молекул на термодинамич. ф-ции, но предполагают, что различия в энергетике однотипных и смешанных взаимод. отсутствуют (Н^Е = 0; G^E = — TS^E). В приближении Флори

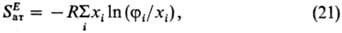
где f_i-объемная доля компонента i, S^E- молярная избыточная энтропия; S^E > 0. Приближение Флори широко используется в теории р-ров полимеров. Развиты подходы, принимающие во внимание не только "объем" молекул, но и их форму.

Наиб. общие решеточные модели учитывают факторы размера и формы молекул, а также энергетич. вклады. При моделировании р-ров с ориентац. эффектами и ассоциацией молекул предполагается, что энергия взаимод. зависит от взаимной ориентации молекул, способа их контактирования. Для контактов разл. типа вводятся разл. энергии взаимообмена (Дж. Баркер, 1953). Решеточные модели, допускающие наличие вакансий в квазирешетке (т. наз. дырочные модели), позволяют рассматривать объемные эффекты в р-рах, получать ур-ние состояния, описывающее не только жидкую, но и паровую фазу. В применении к р-рам развиваются и разл. варианты ячеечных теорий, в к-рых рассматриваются зависимости своб. объема от состава. Для описания ассоциир. р-ров широко применяют теории ассоциативных равновесий, представляющие р-р как смесь мономерных частиц, ассоциатов и сольватов, равновесие между к-рыми определяется действующих масс законом. Смесь таких мол. образований описывается в том или ином приближении, относящемся к системе без специфич. взаимод. (самое грубое приближение-идеальная ассоциир. смесь, затем идет приближение атермич. смеси ассоциатов и т.д.).

В практич. расчетах термодинамич. св-в Р. н., в частности при моделировании фазовых равновесий жидкость-пар, широкое распространение получили т. наз. ур-ния локального состава-ур-ние Вильсона, модели НРТЛ, ЮНИКВАК и др. Для ориентировочного предсказания св-в Р. н. полезны групповые модели, основанные на допущении об аддитивности вкладов разл. групп в избыточные термодинамич. ф-ции (модели ЮНИФАК, АСОГ, квазихимические групповые и др.). В настоящее время развиты модификации моделей, дающие возможность получить ур-ние состояния жидкой и паровой фаз, что особенно важно при расчетах фазовых равновесий в широком диапазоне условий.

80-е гг. 20 в. отмечены успехами в области мол. теории неравновесных св-в р-ров, но трудности здесь еще более серьезные, чем при изучении равновесных св-в.

Лит.: Пригожин И., Дефэй Р., Химическая термодинамика, пер. с англ., Новосиб., 1966; Фиалков Ю. А., Житомирский А.Н., Тарасенко Ю.А., Физическая химия неполных растворов, Л., 1973; Шахпаронов М. И., Введение в современную теорию растворов, М., 1976; Герасимов Я. И., Гейдерих В. А., Термодинамика растворов, М., 1980; Термодинамика разбавленных растворов неэлектролитов, Л., 1982; Белоусов В. П., Панов М. Ю., Термодинамика водных растворов неэлектролитов, Л., 1983; Смирнова Н.А., Молекулярные теории растворов, Л., 1987; Пригожий И. Р., Молекулярная теория растворов, пер. с англ., М., 1990. Н. А. Смирнова.